Sztuczna inteligencja, perceptrony, algorytmy genetyczne – pewnie często słyszałeś te słowa. Coraz więcej rzeczy staje się „inteligentnych”. Sztuczną inteligencję (AI) wsadza się do wszystkiego – telefonów, telewizorów itd. Czy to dobrze? Nie wiem. Lecz na pewno warto wiedzieć, jak to mniej więcej działa. Dlatego w tym artykule przeanalizujemy działanie jednego z algorytmów, który wchodzi w skład bardzo dużej rodziny AI – algorytmu genetycznego. Rozwiążemy za jego pomocą problem komiwojażera.
Problem komiwojażera? Co to jest?
Problem komiwojażera jest jednym z najbardziej charakterystycznych i popularnych problemów optymalizacyjnych współczesnej algorytmiki. Charakteryzuje się on następująco.
Jest sobie pewien człowiek, zwany komiwojażerem. Jak każdy sprzedawca, handluje jakimiś, bliżej nieokreślonymi, towarami. Oczywiście, pragnąłby zarobić jak najwięcej. Musi więc wyruszyć ze swojego domu i odwiedzić wszystkie miasta, które mogą być zainteresowane ofertą. Następnie chciałby wrócić do miasta, z którego zaczął podróż. Komiwojażer musi zarabiać, więc chciałby odwiedzać miasta w takiej kolejności, aby przejechać jak najmniej kilometrów. Dzięki temu oszczędzi na benzynie i więcej zostanie w jego kieszeni.
Problem pozornie może nie wydawać się trudny. Nie będziemy wchodzili tu w zawiłości matematyczne różnych teorii, gdyż to nie jest celem tego artykułu. Przeanalizujemy problem używając jak najprostszych pojęć.
Problem komiwojażera – ilość tras
Jaki byłby najprostszy sposób na znalezienie najkrótszej trasy? Wyznaczenie wszystkich możliwości i wybranie najkrótszej. No jasne – to samo nasuwa się na myśl! Przecież taki sposób zawsze da po pewnym czasie najlepszy wynik. Sprawdźmy na przykładzie.
| Ostrowiec Świętokrzyski | Kielce | Warszawa | Kraków | Poznań | Lublin | |
| Ostrowiec Świętokrzyski | 0 km | 61 km | 177 km | 188 km | 381 km | 104 km |
| Kielce | 61 km | 0 | 177 km | 118 km | 338 km | 165 km |
| Warszawa | 177 km | 177 km | 0 km | 294 km | 296 km | 165 km |
| Kraków | 188 km | 118 km | 294 km | 0 km | 368 km | 255 km |
| Poznań | 381 km | 338 km | 296 km | 368 km | 0 km | 440 km |
| Lublin | 104 km | 165 km | 165 km | 255 km | 440 km | 0 km |
Jakie istnieją możliwe trasy, takie abyśmy rozpoczęli i skończyli w tym samym mieście?
| L.p | Miasto 1 | Miasto 2 | Miasto 3 | Miasto 4 | Miasto 5 | Miasto 6 | Miasto 7 | Dystans |
| 1 | Ostrowiec | Kraków | Kielce | Warszawa | Lublin | Poznań | Ostrowiec | 1469 km |
| 2 | Kraków | Ostrowiec | Kielce | Warszawa | Poznań | Lublin | Kraków | 1417 km |
| 3 | Kielce | Ostrowiec | Kraków | Lublin | Poznań | Warszawa | Kielce | 1417 km |
| 4 | Ostrowiec | Lublin | Poznań | Warszawa | Kielce | Kraków | Ostrowiec | 1323 km |
| 5 | Lublin | Warszawa | Ostrowiec | Poznań | Kraków | Kielce | Lublin | 1374 km |
| 6 | Poznań | Lublin | Kraków | Ostrowiec | Kielce | Warszawa | Poznań | 1417 km |
| 7 | Ostrowiec | Poznań | Warszawa | Kielce | Kraków | Lublin | Ostrowiec | 1331 km |
| … | … | … | … | … | … | … | … | … |
| 360 | Warszawa | Poznań | Kraków | Kielce | Ostrowiec | Lublin | Warszawa | 1197 km |
Jak widzisz – mamy tylko 6 miast. Istnieje między nimi aż 360 unikalnych możliwych połączeń! W tabelce, jak widzisz, nie zostały wypisane wszystkie możliwości. Jak więc wyznaczyć ich ilość?
Zakładając, że możemy wystartować w dowolnym mieście, istnieje n! możliwych tras. Dla przykładu powyżej: Pierwsze miasto możemy wybrać na 6 sposobów, drugie na 5 (gdyż jedno miasto wykorzystaliśmy już na pierwszej pozycji), trzecie miasto na 4 sposoby itd. Efektywnie będzie to 6*5*4*3*2*1=6! możliwych tras. Uprośćmy trochę rozważania i przyjmijmy że trasa O->KR->KI->L->P->O będzie miała taką samą długość jak trasa O->P->L->KI->KR->O (miasta są odwiedzane w odwrotnej kolejności). Dzięki temu możemy ograniczyć nieco ilość sprawdzanych opcji. Ilość tras możemy wyznaczyć za pomocą wzoru:
Jeśli chcemy rozwiązać problem komiwojażera przypadku, gdy miasto startowe zostało określone i jest stałe (np.: Ostrowiec dla powyższego przypadku) – wzór przyjmie następującą postać:
Powyżej opisane zbiory miast są tzw. permutacjami.
Zauważ, że jeśli chcielibyśmy sprawdzić ręcznie każdą możliwą trasę, ilość tras które musimy sprawdzić będzie rosła bardzo szybko. Załóżmy, że dysponujemy komputerem przeliczającym milion operacji na sekundę. Poniższa tabelka przedstawia czas działania algorytmu: (zakładamy że możemy startować w dowolnym mieście
| Ilość miast | Ilość tras | Czas działania algorytmu |
| 10 | 1 814 400 | 1.8s |
| 11 | 19 958 400 | 19s |
| 12 | 239 500 800 | 239s |
| 13 | 3 113 510 400 | 51 minut |
| 14 | 43 589 145 600 | 726 minut |
Z tego powodu powstało wiele metod wyznaczania przybliżonego rozwiązania problemu komiwojażera, które nie wymagają sprawdzania wszystkich możliwych kombinacji. Jednym z takich sposobów jest algorytm genetyczny.
Algorytm genetyczny – na czym polega?
Czym jest algorytm genetyczny? Jest to swego rodzaju „symulacja ewolucji”. Co przez to można rozumieć?
Mamy na początku pewną populację. Ta populacja składa się z osobników. Każdy z nich posiada pewien wskaźnik, który określa jak dobrze jest on przystosowany do życia. Każdy osobnik posiada też swój „kod genetyczny”, który określa w jaki sposób rozwiąże on dany problem.
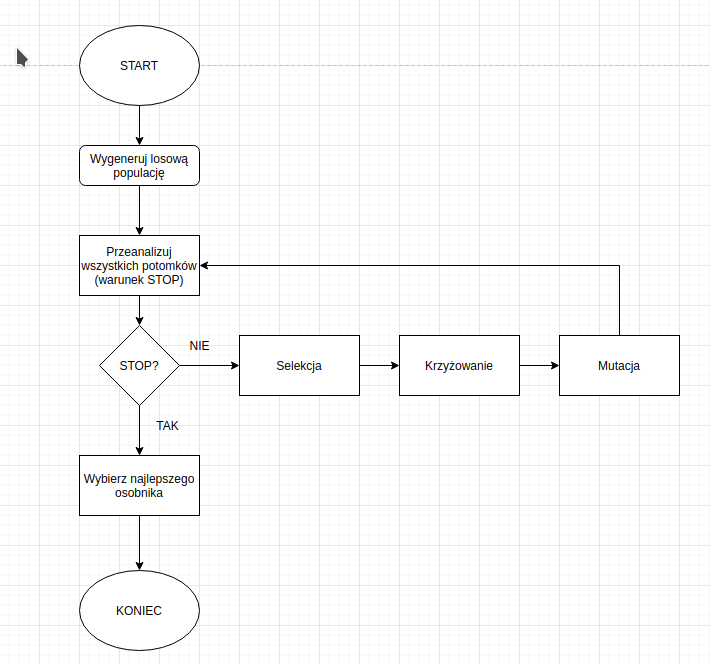
Powyżej znajduje się schemat blokowy przykładowego algorytmu genetycznego. Jak widzisz, nie jest on skomplikowany.
Przygotowanie – w jaki sposób zakodować genom?
Kodowanie jest jednym z najważniejszych etapów opracowywania algorytmu genetycznego rozwiązującego dany problem. Dlaczego? Gdyż właśnie sposób zakodowania informacji w genomie oraz opracowanie funkcji przystosowania decydują o tym, jakiego operatora selekcji czy krzyżowania użyjemy oraz jak dobry będzie nasz algorytm.
Zastanówmy się, w jaki sposób możemy zakodować w sposób jednoznaczny genom pojedynczego osobnika, który pomoże nam rozwiązać problem komiwojażera? Kto będzie w ogóle takim osobnikiem?
Szukamy najbardziej optymalnej trasy, a więc właśnie pojedyncza trasa będzie najlepszym wyborem na naszego „wzorcowego” osobnika. Genomem osobnika będzie natomiast lista miast. Miejscowości oznaczymy sobie kolejnymi liczbami. Odczytując genom od lewej do prawej otrzymamy kolejność w jakiej powinniśmy odwiedzać miasta.
Przygotowanie – warunek stopu
Spójrz na bloczek oznaczony STOP? na wykresie. Jest to nasz warunek stopu. Co to jest? Mówi nam o tym, kiedy nasz algorytm powinien przestać działać. Jeśli nie określimy warunku stopu – algorytm genetyczny będzie wykonywany w nieskończoność.
Jakie mogą być warunki stopu? Przeróżne. Od najprostszych (pokroju ilości iteracji algorytmu) przez bardzo złożone (np.: zatrzymujemy algorytm wtedy, kiedy osiągniemy zadowalające nas wyniki).
Przygotowanie – funkcja przystosowania
Ostatnim krokiem „przygotowawczym” jest opracowanie funkcji przystosowania. Czym jest funkcja przystosowania? Przekazuje nam ona informacje o tym, jak dobry jest konkretny osobnik. Czym jest lepszy, tym wartość funkcji przystosowania powinna być większa.
Funkcja przystosowania powinna być sformułowana w prosty i efektywny sposób. Powinna jasno przekazywać, czy osobnik A jest lepszym kandydatem do reprodukcji, czy jednak osobnik B.
Co będzie najlepszą funkcją przystosowania w naszym wypadku? Zależy nam na tym, aby odnaleziona trasa była jak najkrótsza. Wydaje się intuicyjnie, że to właśnie długość trasy powinna być wskaźnikiem, jak dobry jest dany osobnik.
Jest jedyny drobny problem. W przypadku problemu komiwojażera krótsza trasa (a więc mniejsza wartość) jest lepsza. Natomiast funkcja dostosowania formalnie działa na odwrót. Im większa wartość – tym lepiej. Sformułujemy więc naszą funkcję jako odwrotność całkowitej długości trasy zapisaną w genomie. (funkcja przystosowania=1/całkowita długość trasy)
Etap zerowy – wygenerowanie populacji
W celu zilustrowania przykładami kolejnych etapów algorytmu genetycznego, „wygenerujmy” sobie populację. Załóżmy, że chcemy wyznaczyć najlepszą trasę pomiędzy sześcioma miejscowościami. Załóżmy, że rozmiar naszej populacji wynosi 8. (Oczywiście w rzeczywistej implementacji, im większa ilość osobników w populacji tym szybciej osiągniemy dobre rezultaty) W celu łatwiejszej prezentacji pomnożymy wartość funkcji przystosowania przez 1 000 000 i zaokrąglimy do liczb całkowitych. Dzięki temu nie będziemy męczyli się z ułamkami w przykładach.
Zakodujmy sobie miasta w następujący sposób:
1 – Ostrowiec Świętokrzyski
2 – Kielce
3 – Warszawa
4 – Kraków
5 – Poznań
6 – Lublin
Nasi osobnicy też są znani – to są trasy które zostały już obliczone we wcześniejszej części tego artykułu. Zakodujmy je teraz
| L.p | Miasto 1 | Miasto 2 | Miasto 3 | Miasto 4 | Miasto 5 | Miasto 6 | Wartość funkcji przystosowania |
| A | 1 | 4 | 2 | 3 | 6 | 5 | 681 |
| B | 4 | 1 | 2 | 3 | 5 | 6 | 706 |
| C | 2 | 1 | 4 | 6 | 5 | 3 | 706 |
| D | 1 | 6 | 5 | 3 | 2 | 4 | 756 |
| E | 6 | 3 | 1 | 5 | 4 | 2 | 728 |
| F | 5 | 6 | 4 | 1 | 2 | 3 | 706 |
| G | 1 | 5 | 3 | 2 | 4 | 6 | 751 |
| H | 3 | 5 | 4 | 2 | 1 | 6 | 835 |
Zauważyłeś, że w powyższym kodowaniu nie został „uwzględniony” powrót do miasta początkowego? Zrobiliśmy tak, aby wprowadzić jednoznaczność zapisu. Przy wyliczaniu funkcji przystosowania odległość z miasta 6 do miasta 1 jest oczywiście brana pod uwagę. Przyjmujemy „niejawnie” że zawsze wracamy z miasta odwiedzanego jako ostatnie do miasta odwiedzanego jako pierwsze.
Pierwszy etap algorytmu genetycznego – selekcja
Wg teorii ewolucji jedynie najsilniejsi osobnicy mogą przekazać swoją informację genetyczną potomstwu. Algorytmy genetyczne symulują to zachowanie. Pierwszym etapem działania takiego algorytmu jest selekcja. Na tym etapie wybieramy, które osobniki dostąpią zaszczytu przekazania swoich genów potomstwu. Istnieje wiele metod selekcji, począwszy od najprostszej możliwości, gdzie po prostu wybieramy losowo x osobników, przez bardziej skomplikowane jak metoda ruletki, aż po inne o wiele bardziej rozbudowane metody.
Selekcja turniejowa (tournament selection) – jeden z rodzajów selekcji
Wyróżniłem ten konkretny rodzaj selekcji, gdyż będziemy go używali w przykładowej implementacji. Na czym polega selekcja turniejowa?
W selekcji „turniejowej” uruchamiamy szereg „pojedynków” pomiędzy kandydatami do kolejnego etapu. Z każdego z pojedynków wybieramy „zwycięzcę” i umieszczamy go w populacji końcowej. Jedynie najlepiej „przystosowani” osobnicy przetrwają. Działanie selekcji może być regulowane przez kilka parametrów. Są to przede wszystkim rozmiar turnieju (ile osobników weźmie udział w turnieju) oraz tzw „presja wyboru”. Presja wyboru jest parametrem, który określa prawdopodobieństwo tego, że dany osobnik weźmie udział w danym turnieju. Jeśli osobnik jest słaby, istnieje szansa że do turnieju nawet nie przystąpi, gdyż i tak przegrałby z mocniejszymi kandydatami.
Uruchamiając kolejne turnieje, budujemy populację rodziców, którzy zostaną użyci w kolejnym etapie działania algorytmu.
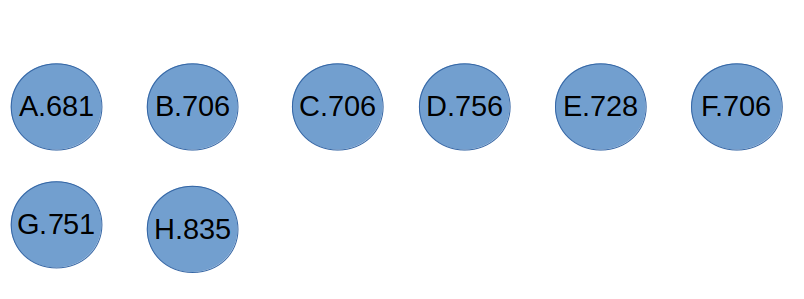
Na powyższym rysunku znajduje się nasza populacja. Każdy osobnik po kropce ma wypisaną wartość funkcji przystosowania. Wybierzmy „losowo” czterech osobników do pierwszego pojedynku.
Pierwszy pojedynek: H.835, G.735, A.681, B.706. Która z tych wartości jest największa? 835. A więc pierwszym z rodziców zakwalifikowanym do etapu krzyżowania będzie rodzic H
Drugi pojedynek: A. 681, G. 751, F.706, C. 706. Największą wartością jest 751, a więc drugim rodzicem zostanie osobnik G.
Drugi etap algorytmu genetycznego – krzyżowanie
Gdy już dobierzemy osobniki, które będą mogły się „rozmnożyć”, będziemy mogli przeprowadzić operację krzyżowania. Czym ona jest? Najprościej rzecz ujmując – bierzemy część „genomu” od pierwszego rodzica i inną część od drugiego rodzica, a następnie łączymy. Dla każdego nowego dziecka liczymy wartość funkcji przystosowania. Z wszystkich potomków, których uzyskamy na drodze krzyżowania tworzymy nową populację.
Krzyżowanie PMX
W naszym algorytmie genetycznym użyjemy krzyżowania PMX. Na czym ono polega? Jest to „troszkę” skomplikowany algorytm, więc niezbędne będą rysunki.
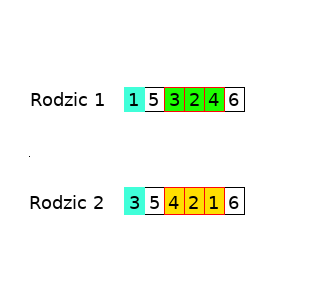
Na początku, jak w każdym krzyżowaniu, mamy dwóch rodziców, którzy posiadają pewny genom. (To są nasi rodzice wybrani w etapie selekcji. Ich genom został przepisany z tabelki wyznaczonej na etapie generowania populacji)

Następnie losujemy dwa punkty – początkowy i końcowy, w których genom zostanie „pocięty”. Załóżmy, że wytniemy fragment od trzeciego (włącznie) do piątego (włącznie) elementu genomu. Oznaczmy wycinane fragmenty czerwoną ramką.
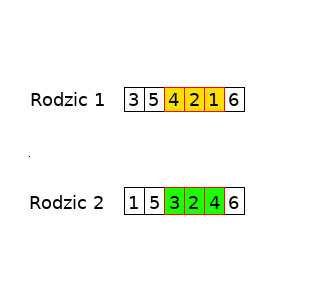
Zamieniamy ze sobą wycięte części. Ta znajdująca się w rodzicu pierwszym (4,2,1) trafia do rodzica drugiego. Natomiast ta z rodzica drugiego trafia do pierwszego.
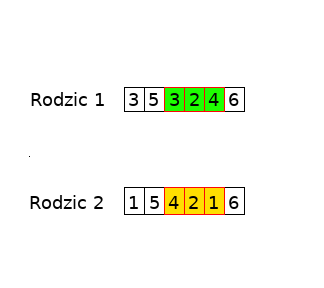
Zauważyłeś, że powstał pewien problem? W rodzicu pierwszym dwa razy występuje miasto nr 3. Natomiast w rodzicu nr 2 występuje podobna sytuacja z miastem nr 1. Jak zaradzić temu problemowi? Pomoże nam w tym „mapowanie”, które zaraz utworzymy.
Zapiszmy sobie, jakie miasta przechodzą w jakie w zamienionych fragmentach:
3->4
2->2
4->1
Mapowanie 2->2 jest całkowicie nieistotne. Zauważmy, że mapowania 3->4 i 4->1 są „przechodnie”. To znaczy: skoro trójka w pierwszym rodzicu przechodzi w czwórkę z drugiego, a czwórka w pierwszym przechodzi w jedynkę. to można powiedzieć że trójka od razu może przejść w jedynkę. Mapowanie takie w ostatecznej postaci będzie wyglądało następująco:
3->4->1 (trójka z pierwszego przechodzi w czwórkę z drugiego rodzica. Natomiast ta czwórka znajdujący się w pierwszym rodzicu przechodzi w jedynkę z drugiego). Efekt: trójka zmieni się w jedynkę.
Co musimy zrobić? Wykonać dodatkową zamianę którą ustaliliśmy dzięki temu mapowaniu!
Otrzymaliśmy dwóch potomków. Obliczamy wartość funkcji przystosowania dla każdego z nich.
Potomek 1: 1331 km -> 1/1331*1 000 000 = 751
Potomek 2: 1112 km -> 1/1112*1 000 000 = 899
Lepszy jest potomek 2, więc to on przejdzie do następnego etapu. Zauważ, że potomek ten jest lepszy także od każdego z dwojga swoich rodziców.
Poniższy filmik dobrze obrazuje sposób działania krzyżowania PMX.
Mutacja – możliwość losowej zmiany genomu
Po krzyżowaniu możemy zmutować genom niektórych osobników. Wykonujemy tę operację jako losową zmianę genomu losowo wybranych osobników. Mutacji poddajemy naprawdę niewielką ilość dzieci, zwykle rzędu 1%. Dlaczego? Ponieważ w przeciwnym wypadku wpłynie to bardzo negatywnie na wyniki algorytmu. Gdy mutacji zostanie poddana większa liczba osobników, traci znaczenie krzyżowanie którego wyniki są niszczone przez mutację.
Dlaczego więc w ogóle przeprowadzamy mutację? Znasz pewnie pojęcie „lokalnego minimum” z lekcji matematyki. Gdy używamy samego krzyżowania, algorytm może utknąć właśnie w takim lokalnym minimum. Dlaczego? Wraz z kolejnymi krzyżowaniami, różnorodność genetyczna osobników staje się coraz mniejsza. W rezultacie możemy dojść do momentu, gdy wszyscy osobnicy w populacji będą mieli dokładnie taki sam genotyp. Mutacja w takim wypadku wpłynie pozytywnie na rozwój populacji, gdyż wzrośnie zmienność genetyczna. Będziemy mogli „wybić” się z tego lokalnego minimum i znaleźć jeszcze lepsze rozwiązanie.
W jaki sposób przeprowadzamy mutację? Najprostszy operator to zamiana dwóch elementów genomu ze sobą.
Co dalej?
Wyznaczyliśmy jeden element, który możemy wstawić do nowej populacji: 3->5->4->2->1->6. Analogicznie wyznaczamy pozostałą część nowej generacji. Gdy otrzymamy już 8 członków, wybieramy najlepszego osobnika i sprawdzamy warunek stopu. Jeśli nas nie zadowala, jedziemy dalej. W przeciwnym wypadku kończymy algorytm.
Mam nadzieję, że zainteresowałem cię tym tematem 🙂 W kolejnej części zajmiemy się praktyczną implementacją algorytmu w języku Typescript, używając frameworka Angular.
Źródła (możesz tu poszerzyć swoją wiedzę)
- https://stackabuse.com/traveling-salesman-problem-with-genetic-algorithms-in-java/
- https://www.geeksforgeeks.org/tournament-selection-ga/
- https://towardsdatascience.com/how-to-define-a-fitness-function-in-a-genetic-algorithm-be572b9ea3b4
- http://www.theprojectspot.com/tutorial-post/applying-a-genetic-algorithm-to-the-travelling-salesman-problem/5