Matura z informatyki 2016 – Liczba PI (C++, arkusz kalkulacyjny)

Czas czytania: 2 minut

Witajcie 🙂 Mam nadzieję, że przygotowujecie się do matury, drodzy czytelnicy? Cofamy się kolejny roczek do tyłu. Bierzemy na warsztat zadanie „Liczba PI” znajdujące się na arkuszu maturalnym w roku 2016. Mamy do rozwiązania jedynie trzy podpunkty. Czy pójdzie gładko? Zobaczymy. No to zaczynajmy 🙂

Jeśli chcesz przeczytać omówienie rozwiązań innych zadań maturalnych z informatyki, zapraszam do odwiedzin specjalnie przygotowanej do tego celu strony. Agreguje ona nie tylko wszystkie omówione do tej pory treści, ale daje łatwy dostęp do arkuszy maturalnych z informatyki oraz ich rozwiązań.

Dobra. Wystarczy już ględzenia. Bierzmy się za robotę i rozwalmy kolejne zadanko z matury 🙂

Zadanie 4. Liczba PI

W kartezjańskim układzie współrzędnych na płaszczyźnie narysowano kwadrat o boku długości 400 i środku symetrii w punkcie (200;200). Boki kwadratu są równoległe do osi układu współrzędnych. W kwadrat wpisano koło. Następnie wylosowano 10 000 punktów należących do kwadratu. Współrzędne (x,y) punktów zostały zapisane w pliku punkty.txt Każdy punkt w osobnym wierszu. Wiersz ma postać dwóch liczb całkowitych z zakresu <0;400>, rozdzielonych pojedynczym znakiem odstępu.

Korzystając z powyższych danych oraz dostępnych narzędzi informatycznych, wykonaj zadania. Wyniki zapisz w pliku tekstowym wyniki_4.txt. Odpowiedź do każdego zadania poprzedź numerem zadania.

Kod uniwersalny dla wszystkich podpunktów

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

const int MIDDLEX = 200;
const int MIDDLEY = 200;
const int R = 200;
struct Point {
int x;
int y;
};

vector<Point> loadPointsFromFile(string filename) {
vector<Point> data;
ifstream file;
file.open(filename);
if(file.is_open()==false) {
cout<<"Nie udało się otworzyć pliku "<<filename<<endl;
return data;
}
for(int i = 0;i<10000;i++) {
struct Point pp;
file>>pp.x;
file>>pp.y;
data.push_back(pp);
}
return data;
}

Na samym początku tworzymy sobie trzy stałe. Określają nam one środek okręgu oraz jego promień. Następnie napisaliśmy sobie strukturkę, w której będziemy przechowywali informacje na temat pojedynczego punktu.

Funkcja odczytująca plik wygląda standardowo, podobnie jak w omówieniu zadania z 2017 i 2018 roku. Na początku tworzymy vector, w którym będziemy przechowywali odczytane dane. Otwieramy plik. Sprawdzamy, czy ta operacja sie udała. Jeśli się udała, to odczytujemy 10000 współrzędnych z pliku. Korzystamy ze strumieni, gdyż w tym wypadku to one są najwygodniejsze. Na samym końcu funkcji zwracamy pobrane punkty.

Zadanie 4.1. (0-3)

Wypisz współrzędne tych punktów, które należą do brzegu koła (okręgu), oraz podaj liczbę punktów należących do wnętrza koła (brzeg koła nie należy do wnętrza koła).

Wskazówka:

Równanie okręgu o środku w punkcie S = (a,b) i promieniu r > 0 ma postać:

(x-a)^2+(y-b)^2=r^2

Informacja

W pliku wśród 100 pierwszych punktów 80 należy do wnętrza koła.

Rozwiązanie

34
35
36
37
38
39
40
41

bool isOnTheCircumference(Point p) {
if((pow(p.x-MIDDLEX,2)+pow(p.y-MIDDLEY,2))==(R*R)) return true;
return false;
}
bool isInTheCircle(Point p) {
if((pow(p.x-MIDDLEX,2)+pow(p.y-MIDDLEY,2))<(R*R)) return true;
return false;
}

Jak na najprostsze zadanie przystało, nic szczególnego. CKE podało nam na tacy wszystkie wzory. Wystarczy tylko odpowiednio z nich skorzystać.

Co zrobiliśmy w powyższym listingu? Utworzyliśmy dwie funkcje pomocnicze. Pierwsza sprawdza, czy punkt znajduje się na krawędzi koła. Korzystamy tam z podanego w treści polecenia wzoru. Sprawdzamy, czy jest on prawdziwy. Jeśli tak, oznacza to że punkt leży na krawędzi koła. Zwracamy wtedy true.

Druga funkcja jest stworzona analogicznie. Tym razem jednak warunek jest inny. Sprawdzamy, czy lewa część wzoru jest mniejsza od prawej. Dlaczego? Wynika to po prostu z matematyki. Jeśli punkt leży w środku koła oznacza to, że musi leżeć w odległości mniejszej od środka niż promień tego koła. Właśnie dlatego zastosowaliśmy w funkcji znak mniejszości.

42
43
44
45
46
47
48
49
50
51
52

int main()
{
vector<Point> data = loadPointsFromFile("punkty.txt");
int inTheCircleCount = 0;
for(Point pt : data) {
if(isInTheCircle(pt)==true) inTheCircleCount++;
if(isOnTheCircumference(pt)) cout<<"("<<pt.x<<","<<pt.y<<"),";
}
cout<<inTheCircleCount;
return 0;
}

Wyjątkowo przeanalizujemy funkcję main. Co tutaj się znajduje? Na samym początku oczywiście wczytujemy dane z pliku. Tworzymy zmienną pomocniczą w której będziemy zliczali ilość punktów lężących wewnątrz koła. Następna część kodu to range-based for. Rozwiązujemy jednocześnie obydwa podpunkty zadania. Sprawdzamy, czy punkt znajduje się wewnątrz koła. Jeśli tak – zwiększamy wartość zmiennej inTheCircleCount o 1. Podobnie weryfikujemy, czy punkt należy do krawędzi koła. Jeśli tak, wypisujemy jego współrzędne. (Oczywiście, nie zapominamy o przepisaniu ich ręcznie do pliku wyniki_4.txt, z odpowiednią adnotacją na temat zadania)

Kompletne rozwiązanie zadanie 4.1

Zadanie 4.2 (0-3)

Przy założeniu równomiernego rozkładu punktów w kwadracie, stosunek liczby punktów należących do koła do liczby punktów należących do kwadratu w przybliżeniu równy jest stosunkowi pola koła Pk do pola kwadratu P.

Wyznacz przybliżoną wartość liczby pi, biorąc pod uwagę punkty z pliku punkty.txt:

pierwszych 1000 punktów
pierwszych 5000 punktów
wszystkie punkty

Wynik zaokrąglij do 4 miejsc po przecinku.

Wzór:

$\frac{n_{k}}{n}\approx \frac{P_{k}}{P}$

Rozwiązanie:

No cóż. Matematyka jest królową nauk. Nie rozwiążemy tego zadania, jeśli nie będziemy potrafili przekształcić powyższego wzoru. Pamiętasz jak liczy się pole koła, prawda? Ta wiedza w tym momencie naprawdę się przyda. Jeśli za żadne skarby świata nie możesz sobie przypomnieć takiego wzoru, spójrz poniżej 🙂

$P_{k}= \pi*r^2$

Przeprowadźmy przekształcenie wzorów. Musimy wyznaczyć wartość liczby PI.

$\frac{n_{k}}{n}\approx \frac{\pi * r^2}{P}$

$n* \pi * r^2 \approx n_k * P$

$\pi=\frac{n_k * P}{n * r^2}$

Napiszmy teraz program, który skorzysta z wyliczonego powyżej wzoru.

36
37
38
39

bool isBelongToTheCircle(Point p) {
if((pow(p.x-MIDDLEX,2)+pow(p.y-MIDDLEY,2))<=(R*R)) return true;
return false;
}

Ta funkcja powinna wydać ci się znajoma… TAK. To prawie ta sama, którą napisaliśmy w odpowiedzi na poprzedni podpunkt zadania. Czym się różni? Wcześniej musieliśmy oddzielnie wyznaczyć punkty leżące na krawędzi koła oraz należące do wnętrza koła. Przy wyliczaniu wartości PI uznajemy, że do koła należą zarówno te punkty które znajdują się na jego obrysie jak i te, które położone są wewnątrz. Dlatego instrukcja warunkowa zmieniła się.

40
41
42
43
44
45
46
47
48

double calculateRatio(int circlePoints,int numberOfPoints) {
const double circleArea = M_PI*(R*R);
const double squareArea = (2*MIDDLEX)*(2*MIDDLEY); // lub po prostu 400*400

double numerator = circlePoints*squareArea;
double denominator = numberOfPoints*R*R;
double result = numerator/denominator;
return result;
}

Funkcja calculateRatio wylicza liczbę pi wg wzoru, który ustaliliśmy na początku. Jako argument przyjmujemy ilość punktów, znajdujących się wewnątrz koła, a także ilość punktów dla których chcemy przeprowadzić wyliczenia. Najpierw tworzymy sobie dwie stałe. Pierwsza z nich zawiera pole koła. (W tym miejscu z niego skorzystaliśmy metodą kopiuj-wklej). Druga stała to pole kwadratu, który jest opisany na tym kole.

Wyliczanie ułamka rozbiliśmy sobie na dwa kroki. Najpierw obliczamy licznik (zmienna numerator), a następnie mianownik. Ponownie stosujemy metodę copy-paste. Podstawiamy nasze wyliczone wcześniej zmienne pod wyznaczony wzór.

Zmienna result zawiera odpowiedź do zadania (dla danej liczby punktów)

49
50
51
52
53
54
55
56

double calculatePIAccuracy(vector<Point>& data,int numberOfPoints) {
int inTheCircleCount = 0;
for(int i = 0;i<numberOfPoints;i++) {
if(isBelongToTheCircle(data[i])==true) inTheCircleCount++;
}
double result = calculateRatio(inTheCircleCount,numberOfPoints);
return result;
}

Funkcja calculatePIAccuracy służy do ustalenia ostatecznego wyniku. Jako argumenty przyjmujemy vector z punktami oraz liczbę punktów, które chcemy wziąć pod uwagę przy wyliczaniu liczby PI.

Liczbę punktów znajdujących się wewnątrz koła obliczamy podobnie, jak w poprzednim zadaniu. Zmienna pomocnicza inTheCircleCount, pętla for (dlaczego nie range-based? Ponieważ zadanie wymaga od nas przejścia określonej części tablicy) i inkrementacja gdy warunek jest spełniony. Następnie korzystamy z funkcji calculateRatio, która odwala całą brudną robotę.

56
57
58
59
60
61
62
63
64

int main()
{
vector<Point> data = loadPointsFromFile("punkty.txt");
cout<<std::fixed;
cout<<std::setprecision(4)<<calculatePIAccuracy(data,1000)<<endl;
cout<<std::setprecision(4)<<calculatePIAccuracy(data,5000)<<endl;
cout<<std::setprecision(4)<<calculatePIAccuracy(data,10000)<<endl;
return 0;
}

Spójrzmy na funkcję main().

Mamy wyświetlić wynik z dokładnością do czterech miejsc po przecinku. Służy do tego funkcja setPrecision. Jako argument przyjmuje ilość miejsc po przecinku, które chcemy wyświetlić. Używamy na początku fixed aby zmusić strumień do trzymania się naszych zaleceń.

Kompletne rozwiązanie - zadanie 4.2

Zadanie 4.3 (0-5)

Błąd bezwzględny przybliżonej wartości liczby pi, wyznaczonej z n punktów, definiujemy następująco:

$\epsilon_n = | \pi - pi_n |$

Pierwsza zmienna to wartość liczby pi będąca wynikiem standardowej funkcji z narzędzia informatycznego, z którego korzystasz. Druga natomiast – przybliżona wartość liczby pi wyznaczona z n kolejnych punktów, poczynając od pierwszego punktu z pliku punkty.txt

Oblicz błąd bezwzględny dla n=1,2,3… 1700. Na podstawie powyższego zestawienia utwórz wykres liniowy ilustrujący zmiany dokładności wyznaczanej liczby pi. Zadbaj o czytelność wykresu. Wartości dla n=1000 i n=1700 (zaokrąglone do czterech liczb do przecinku) zapisz do pliku wyniki_4.txt

Rozwiązanie:

Mamy utworzyć wykres liniowy … Powinno ci w głowie zaświtać, że sam C++ do tego nie wystarczy … Ale po kolei.

Najpierw wyznaczmy błąd bezwzględny dla n=1,2,3 … 1700.

56
57
58

double calculateAbsoluteError(double pi) {
return fabs(M_PI-pi);
}

Obliczenie błędu bezwzględnego to po prostu podstawienie do wzoru. Nic szczególnego. Zmienna pi zawiera wartość wyliczoną przez nasz program. Natomiast M_PI to stała z biblioteki cmath, zawierająca dokładną wartość liczby PI. Używamy funkcji fabs, gdyż operujemy na liczbach zmiennoprzecinkowych.

60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

void writeAbsoluteErrorsToFile(string filename,string filename2,vector<Point> &data) {
ofstream file;
ofstream file2;
file.open(filename);
file2.open(filename2);
if(file.is_open()==false || file2.is_open()==false) {
cout<<"Nie udało się otworzyć pliku"<<endl;
return;
}
file<<std::fixed<<std::setprecision(4);
file2<<std::fixed<<std::setprecision(4);
for(int i = 1;i<=1700;i++) {
file<<calculateAbsoluteError(calculatePIAccuracy(data,i))<<endl;
if(i==1000 || i==1700) file2<<calculateAbsoluteError(calculatePIAccuracy(data,i))<<endl;
}
}

Funkcja przedstawiona powyżej zapisuje wymagane przez polecenie informacje do pliku. Możesz się zastanowić, po co nam dwa pliki? W jednym z nich (filename) zapisywane są wszystkie wygenerowane dokładności liczby pi, dla n z zakresu <1,1700>. Jego zawartość będzie nam potrzebna w następnym kroku do wygenerowania wykresu. Drugi plik to spełnienie żądań egzaminatorów z CKE. Zapisujemy w nim En1000 i En1700 z dokładnością do 4 miejsc po przecinku. (Pamiętajmy o przekopiowaniu treści tego pliku do wyniki_4.txt, z odpowiednią adnotacją :))

Do wyliczenia błędu bezwzględnego używamy utworzonej przed chwilą funkcji calculateAbsoluteError. Jako argument przekazujemy funkcję calculatePIAccuracy, która zwraca wyznaczoną wartość liczby pi dla określonej liczby punktów.

Rozwiązanie działa prawidłowo i nadaje się na maturę. Jako zadanie domowe pozostawiam ci optymalizację. Przypomnij sobie jak działa funkcja calculatePIAccuracy. Przeanalizuj, jak dużo nadmiarowych obliczeń wykonujemy, używając jej w ten sposób. Zastanów się, jak można ją poprawić aby nie marnować tyle mocy obliczeniowej.

Tworzenie wykresu

Po skopiowaniu liczb z wygenerowanego pliku i wklejeniu ich do LibreOffice Calc ukaże nam się następujące okienko:

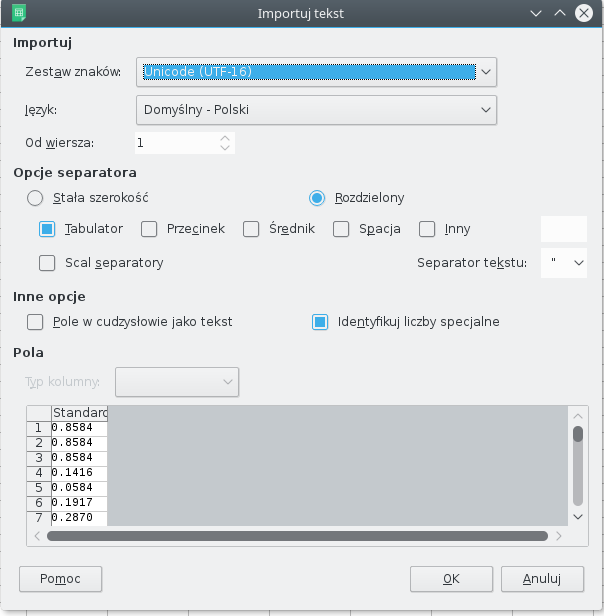
Musimy wskazać, w jaki sposób program ma obsłużyć wklejone liczby. Nic nie musimy zmieniać. (Excel również nie powinien mieć problemów z interpretacją).

Zauważymy natomiast jeden problem. Arkusz kalkulacyjny interpretuje wklejone liczby jako tekst! Dzieje się tak, gdyż C++ przy zapisie do pliku użył kropki do oddzielenia części ułamkowej. Natomiast programy kalkulacyjne wolą przecinek. Możemy prosto naprawić tę niedogodność. Klikamy Edycja->Znajdź i zamień. W okienku jako znajdź wpisujemy kropeczkę, a jako zamień przecinek. Klikamy zamień wszystkie.

Następnym krokiem jest wygenerowanie wykresu.

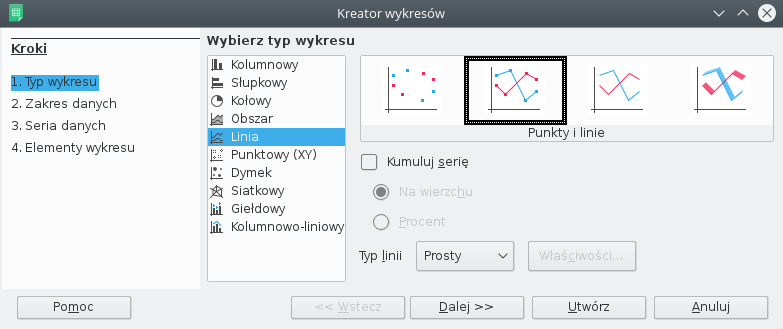
Najbardziej dostosowany do naszych potrzeb będzie wykres liniowy.

Na ekranie: Zakres danych nie ustawiamy nic.

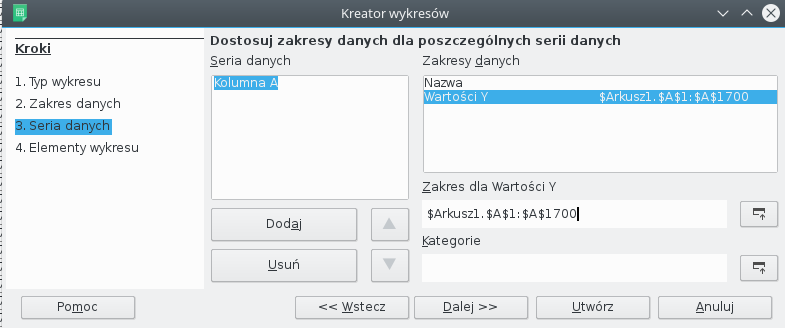
Kolejny etap to dodanie serii danych. Klikamy przycisk dodaj. Następnie ustawiamy zakres wartości Y. Klikamy przycisk z symbolem arkusza i plusa po prawej stronie pola edycyjnego. Wybieramy komórki, w które wkleiliśmy liczby (w moim wypadku to komórki od A1 do A1700). Klikamy Utwórz.

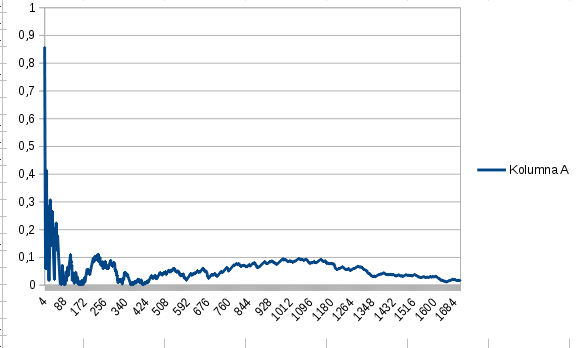
Voila: Wykres gotowy 🙂 Możemy pobawić się w poprawę jego wyglądu i dodanie opisów, legend. Taki wynik naszej pracy powinien zostać bezproblemowo zaakceptowany przez CKE.

Gratulacje 🙂

Czytając ten wpis, wykonałeś kolejny krok w procesie przygotowania się do matury z informatyki. Niebawem ukażą się kolejne edukacyjne treści. Będziemy rozwiązywali zadania z programowania z ubiegłych lat. Jak omówimy wszystkie matury z informatyki pod względem programowania, zajmiemy się kolejnymi rodzajami zadań.

Jeśli masz jakieś uwagi, zauważyłeś jakiś błąd, pisz śmiało 🙂 Jestem otwarty na konstruktywne opinie i komentarze.

Tym czasem – do zobaczenia 🙂 Zachęcam do lektury pozostałych wpisów. Spis matur oraz omówionych do tej pory zadań znajduje się tutaj.

Niestety, nie mamy jeszcze podobnych artykułów do tego, który właśnie przeczytałeś :( Zajrzyj w przyszłości, a na pewno coś się znajdzie :)

Zadanie 4. Liczba PI

Kod uniwersalny dla wszystkich podpunktów

Zadanie 4.1. (0-3)

Rozwiązanie

Zadanie 4.2 (0-3)

Rozwiązanie:

Zadanie 4.3 (0-5)

Rozwiązanie:

Gratulacje 🙂

Dodaj komentarz Anuluj pisanie odpowiedzi